
Chaos and Context
“Watch two bits of foam flowing side by side at the bottom of a waterfall. What can you guess about how close they were at the top? Nothing. As far as standard physics was concerned, God might just as well have taken all those water molecules under the table and shuffled them personally. Traditionally, when physicists saw complex results, they looked for complex causes. When they saw a random relationship between what goes into a system and what comes out, they assumed that they would have to build randomness into any realistic theory, by artificially adding noise or error. The modern study of chaos began with the creeping realization in the 1960s that quite simple mathematical equations could model systems every bit as violent as a waterfall. Tiny differences in input could quickly become overwhelming differences in output — a phenomenon given the name “sensitive dependence on initial conditions.” In weather, for example, this translates into what is only half-jokingly known as the Butterfly Effect — the notion that a butterfly stirring the air today in Peking can transform storm systems next month in New York.” — James Gleick in the prologue to ‘Chaos’
Around 2010, when I was starting to become really interested in game design, I had another paired obsession: chaos and complexity theory. The two were sort of hand-in-hand for a long time, and related in obvious ways.
The above quote comes from the book that introduced me to chaos, but my research over the next few years blossomed into dozens of books, correspondences, seminars. There is something so beautiful about the sort of indescribable behavior of complex systems like fire, clouds, steam, water, where you can tell intuitively there is some pattern or logic to the motion, but it is so chaotic and unpredictable it almost feels like you’re looking at another thinking being, something totally outside of your comprehension with its own desires and impulses. And especially to a young game designer, it’s overwhelming to understand that those behaviors are caused entirely by small, simple rulesets acting ‘predictably.’
During this time I saw myself more as a student than an artist, and if I was working on a game there was likely some theory or practical concept I was dealing with alongside. So when I started Tenderfoot Tactics, I had some goals. I wanted chaotic and complex behavior to exhibit itself unavoidably in the systems. My theory going in was that if the inputs and outputs of player actions all shared a spatial context, chaotic behavior would be more likely. If you perform an action, it should change the board state in a way that changes the way you’d think about your next action. And then that the sheer density of those interactions would create chaos. But it was just a theory and I wanted to develop it, to understand how to design for beautiful chaos and complex, unpredictable behavior from simple and deterministic systems.
One book that had sat on my shelf menacingly through this period was A New Kind of Science by Stephen Wolfram. NKS is an incredibly threatening book. My copy is hardcover, large-textbook size, about 1200 pages long before the index. I thought I’d need a project to help me get through it, so around the time I was starting Tenderfoot in late 2014, I decided to try to start a journal: a critical read of NKS from the perspective of a game designer wanting to better understand how to design complex systems, looking for practically applicable bits and pieces I could bring back to our field.
NKS is essentially a long and very detailed report of the results of 20 years of experimental studies on complexity in cellular automata. Wolfram would create some boundaries around the types of rules that would be permitted in a test set, and then try literally every possible combination of rules (even if that meant thousands or millions of tests) and detail their outcomes, searching for programs that generate surprising results. It’s an incredible book. Given that complexity is what I’m after in my games, and given the shared spatial grid nature of tactics games and cellular automata, it seemed clear I’d find something of use here.
Well, it’s been nearly 6 years since I started Tenderfoot, and I still haven’t made it very far through NKS. My ‘loose read’ bookmark is about halfway through, but my ‘close read’ notes go less than 200 pages deep. The reading ahead I’ve done makes me think that the latter half will be less generally useful, but I don’t want to rush through it. Maybe this is as far as this blog series (?) will go but it’s possible this will be a multi-decade process of creation and reflection and digestion as I develop as a game designer.
What I have read of NKS has significantly impacted how I think about designing for complexity, and given that Tenderfoot’s out now, it seems like a good place to at least put a stopper in it for now and get my thoughts out there. I hope to continue the read and post another segment of this blog in the future (maybe alongside my next tactics game), but I wouldn’t be surprised if the most important core takeaways are already laid out for me in this first chunk. To be honest, it’s partially because of my takeaways from the first chunk of NKS that I’ve spent less time recently focusing on it: it’s felt more and more like my games would benefit more from me working on other parts of myself. But I don’t want to leave this chunk unpublished regardless.
The next section of this blog contains my journal, which is largely pulled-out quotes from the book itself, with some commentary or digestion from me occasionally. I’ll leave it in its current state for now, and I’ll meet you again on the other side, where I’ll tell you what my takeaways are.
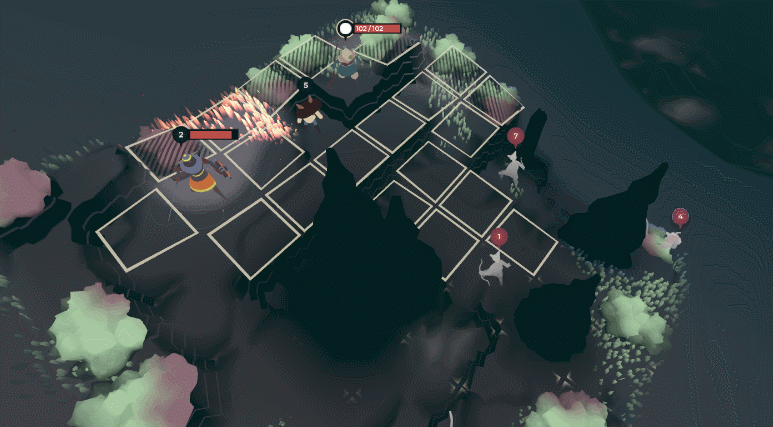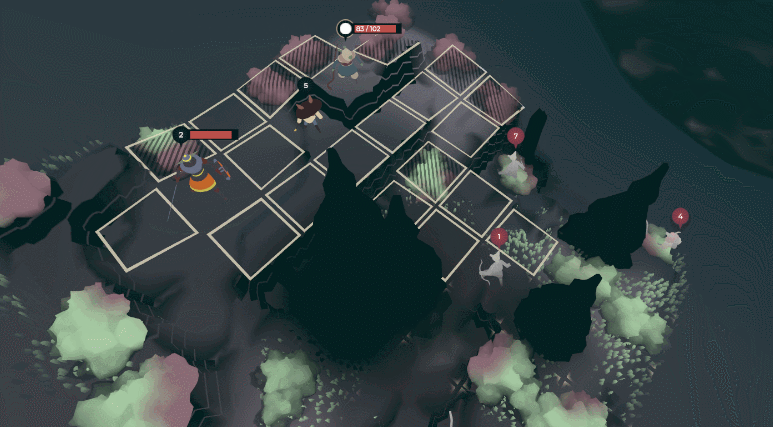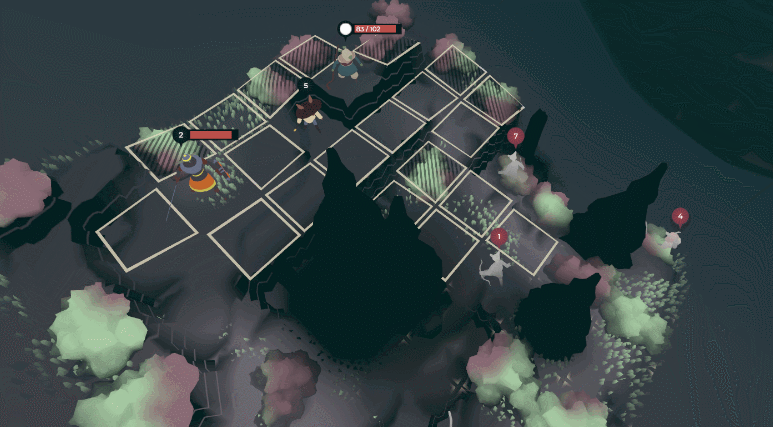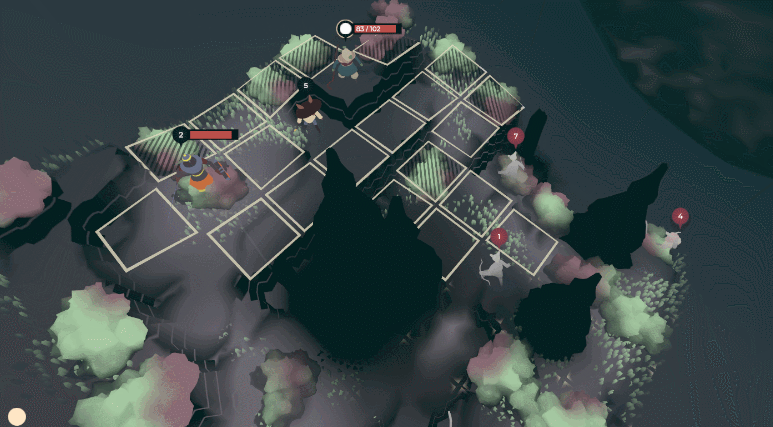
The natural sims in Tenderfoot Tactics (seen here run at 4x speed) are modeled via cellular automata.
An Abbreviated Game Design Critical Read: A New Kind of Science (Stephen Wolfram, 2002)
Chapter 1: The Foundations for a New Kind of Science
“Some of the very simplest programs that I looked at had behavior that was as complex as anything I had ever seen” (2). “All it takes is that systems in nature operate like typical programs and then it follows that their behavior will often be complex. And the reason that such complexity is not usually seen in human artifacts is just that in building these we tend in effect to use programs that are specially chosen to give only behavior simple enough for us to be able to see that it will achieve the purposes we want.” (3)
Complexity in life is actually an unsurprising result that requires little general explanation. Past a very low threshold of interdependent moving parts (like 3 or 4), a randomly selected program may generate infinite complexity and richness.
“Even a program that may have extremely simple rules will often be able to generate pictures that have striking aesthetic qualities — sometimes reminiscent of nature, but often unlike anything ever seen before.” (11)
2 The Crucial Experiment
“If one … looks at simple arbitrarily chosen programs … how do such programs typically behave?” (23)
He identifies four main categories of behavior:
- Uniform
- Repetitive
- Intricate and nested
- Irregular and complex
“Our everyday experience has led us to expect that an object that looks complicated must have been constructed in a complicated way.” Our normal intuition “is mostly derived from experience with building things and doing engineering” where “normally we start from whatever behavior we want to get, then try to design a system that will produce it. Yet to do this reliably, we have to restrict ourselves to systems whose behavior we can readily understand and predict — for unless we can foresee how a system will behave, we cannot be sure that the system will do what we want.” (40)
3 The World of Simple Programs
“I specifically chose the sequence of systems in this chapter to see what would happen when each of the various special features of cellular automata were taken away. And the remarkable conclusion is that in the end none of these features actually matter much at all. For every single type of system in this chapter has ultimately proved capable of producing very much the same kind of complexity that we saw in cellular automata. “So this suggests that in fact the phenomenon of complexity is quite universal — and quite independent of the details of particular systems.
“But when in general does complexity occur?
“The examples in this chapter suggest that if the rules for a particular system are sufficiently simple, then the system will only ever exhibit purely repetitive behavior. If the rules are slightly more complicated, then nesting will also often appear. But to get complexity in the overall behavior of a system one needs to go beyond some threshold in the complexity of its underlying rules.
“The remarkable discovery that we have made, however, is that this threshold is typically extremely low.” (105–106)
Some complexity thresholds discussed in the chapter:
In his one dimensional, boolean cellular automata framework, which he uses primarily throughout the book, there are 256 possible rulesets. ~66% of patterns remain a fixed size. In the remainder, patterns grow forever. About 14% of rulesets yield complex, non-repetitive patterns. 10/256 yield apparent randomness. Rule 110 (and it’s left/right black/white inverses) is (are) the only rulesets which yield “a complex mixture of regular and irregular parts.” So even if the threshold of rule complexity for resultant complexity is low, interesting rulesets are rare. (57)
In three-color totalistic 1D automata, ~85% are repetitive (comparable to what’s implied by the 14% non-repetitive number quoted above). (65)
Next are his simplest mobile automata, which are “similar to cellular automata except that instead of updating all cells in parallel, they have just a single ‘active cell’ that gets updated at each step — and then they have rules that specify how this active cell should move from one step to the next” (71). “Of the 65536 possible … not a single one shows more complex behavior” (than purely repetitive) (73).
Updating the mobile automata rules so that the active cell updates its neighbor cells colors too, we cross the threshold, but just barely. “Once in every few thousand rules, one sees … a kind of nested structure” (73). It takes searching through a few million rules for Wolfram to find the complex randomness he was looking for in these rulesets. He digs into this difference in magnitude by analysing generalized mobile automata as a comparison, which are similar except that there can be more than one active cell at a time. RE: these, “a certain theme emerges: complex behavior almost never occurs except when large numbers of cells are active at the same time. Indeed there is, it seems, a significant correlation between overall activity and the likelihood of complex behavior” (76).
In Turing machines with boolean states on a boolean tape, “repetitive and nested behavior are seen to occur, though nothing more complicated is found” (78). With three states, still nothing complex. Four states is the threshold, with about five per million rulesets of this kind producing randomness. With five, he claims that “apparent randomness becomes slightly more common, but otherwise the results are essentially the same.”
Substitution systems cross the threshold at 3 possible states (2 doesn’t) (86).
In sequential substitutions, the threshold is 3 possible replacements (90).
In tag systems, the threshold is “two elements removed at each step” (93).
Cyclic tag systems are over the threshold in their simplest incarnation.
In register machines (similar to processor architectures) with two registers, the threshold is crossed when rulesets become at least 8 instructions long, though they’re extremely rare (126 / 11 bil).
“The crucial ingredients that are needed for complex behavior are, it seems, already present in systems with very simple rules, and as a result, nothing fundamentally new typically happens when the rules are made more complex.” “Even with highly complex rules, very simple behavior still often occurs.” (106)
Notably, highly complex pseudo-randomness, when averaged and looked at from a grander perspective, is what Wolfram thinks composes the smooth gradients in nature. So extremely high complexity may eventually filter out into soft apparent-simplicity.
With regards to the process of hunting for those simple programs which result in interesting complexity, “it is usually much better … to do a mindless search of a large number of possible cases than to do a carefully crafted search of a smaller number. For in narrowing the search one inevitably makes assumptions, and these assumptions may end up missing the cases of greatest interest.” (111)
4 Systems Based on Numbers
“Traditional mathematics […] assumes that numbers are elementary objects whose only relevant attribute is their size. But in a computer, numbers are not elementary objects. Instead, they mus be represented explicitly, typically by giving a sequence of digits.” (116)
“Start with the number 1 and then just progressively add 1. […] The sizes of these numbers obviously form a very simple progression.
“But if one looks not at these overall sizes, but rather at digit sequences, then what one sees is considerably more complicated. […] These successive digit sequences form a pattern that shows an intricate nested structure.” (117)
This seems like a trick at first but I think it may actually be profound, that a different view on the same system can turn apparent simplicity into apparent complexity.
“The rules for cellular automata are always local: the new color of any particular cell depends only on the previous color of that cell and its immediate neighbors. But in systems based on numbers there is usually no such locality. […] Most simple arithmetic operations have the property that a digit which appears at a particular position in their result can depend on digits that were originally far away from it.
But despite fundamental differences like this in the underlying rules, the overall behavior produced by systems based on numbers is still very similar to what one sees for example in cellular automata.”
Note that there are many examples I have excluded for brevity, and while addition is rather local, most operations are not, and still exhibit complexity. I think it is worth noting that there is still meaning in the spatial relationships between digits, even if the rules don’t require digits be near each other to influence one another.
“So far in this chapter we have always used digit sequences as our way of representing numbers. But one might imagine that perhaps […] if we were just to choose another one, then numbers generated by simple mathematical operations would not longer seem complex.”
“In thinking about representations of numbers, it seems appropriate to restrict oneself to cases where the effort required to find the value of a number from its representation is essentially the same for all numbers. If one does this, then the typical experience is that in any particular representation, some class of numbers will have simple forms. But other numbers, even though they may be the result of simple mathematical operations, tend to have seemingly random forms.
And from this it seems appropriate to conclude that numbers generated by simple mathematical operations are often in some intrinsic sense complex, independent of the particular representation that one uses to look at them.” (142–144)
-
An abrupt conclusion
Some takeaways:
Complexity is actually an unsurprising result of systems. The reason we see it as surprising is because we’re used to (human engineered) systems that have been designed to be predictable and simple. Without intentional design, complexity will emerge naturally.
A perfectly simple program will never generate complexity, but the threshold for how complex a ruleset needs to be to generate a complex outcome, that threshold is very low (like 3–4 interacting elements), and after passing it, there is no apparent benefit (nor detriment) to the rules being more complex, w/r/t the complexity of outcome.
It is better to go searching for complexity randomly than to look where you expect it. It will be in the rules you don’t expect that the most surprising complexity will be found.
What looks like simplicity from one perspective may be complexity when seen through a different lens.
Digested for my own practice:
Don’t fixate on designing a system within certain boundaries when searching for complexity. Wherever you go looking, if you look long enough or from the right perspectives, you’ll find complexity.
For me, this has meant letting fiction and fantasy and intuition guide my design practice, not to design intending complexity but instead to look for complexity as we go and to nurture and cherish what we bump into on accident.
It’s also supported a growing belief that simplicity of rules is an aesthetic preference and, to some degree, an accessibility concern, but that generally it is not linked to complexity of outcomes, and I’m less and less concerned about that kind of ‘elegance’ in my design. Actually NKS’ observation that complex behavior viewed from far enough back can often look like a soft gradient makes me curious about whether there are aesthetics of soft chaos available to large and messy games that aren’t visible in simple and elegant ones.
Going forward I hope to build on Tenderfoot’s design in my next project by focusing more on fiction and fantasy and feeling as guiding lights, and letting the complexity be found rather than sought.
November 1, 2020